Hungarian Algorithm for Assignment Problem

What is Hungarian method?

The Hungarian strategy is a computational streamlining method that tends to the task issue in polynomial time and foretells following basic double other options. In 1955, Harold Kuhn utilized the expression "Hungarian technique" to respect two Hungarian mathematicians, Dénes Konig and Jeno Egerváry. The Hungarian Method depends on the rule that assuming that a consistent is added to each component of a line as well as a segment of cost framework, the ideal arrangement of the subsequent task issue is equivalent to the first issue as well as the other way around.

What is an Assignment Problem?

A transportation issue is a sort of task issue. The objective is to allot an equivalent measure of assets to similar number of exercises. Subsequently, the general expense of designation is limited or the complete benefit is amplified.

Since accessible assets like labourers, machines, and different assets have fluctuating levels of effectiveness for executing various exercises, and consequently the expense, benefit, or loss of leading such exercises changes.

Accept we have 'n' tasks to take care of on 'm' machines (i.e., one occupation to one machine). We want to dole out positions to machines for minimal measure of cash conceivable (or most extreme benefit). In light of the idea that each machine can achieve each undertaking, yet at variable degrees of effectiveness.

Purpose of Hungarian Algorithm

The Hungarian Algorithm is utilized to find the base expense in task issues that include relegating individuals to exercises. To utilize this calculation, we start by sorting out our information into a grid with individuals as the lines and exercises as the segments.

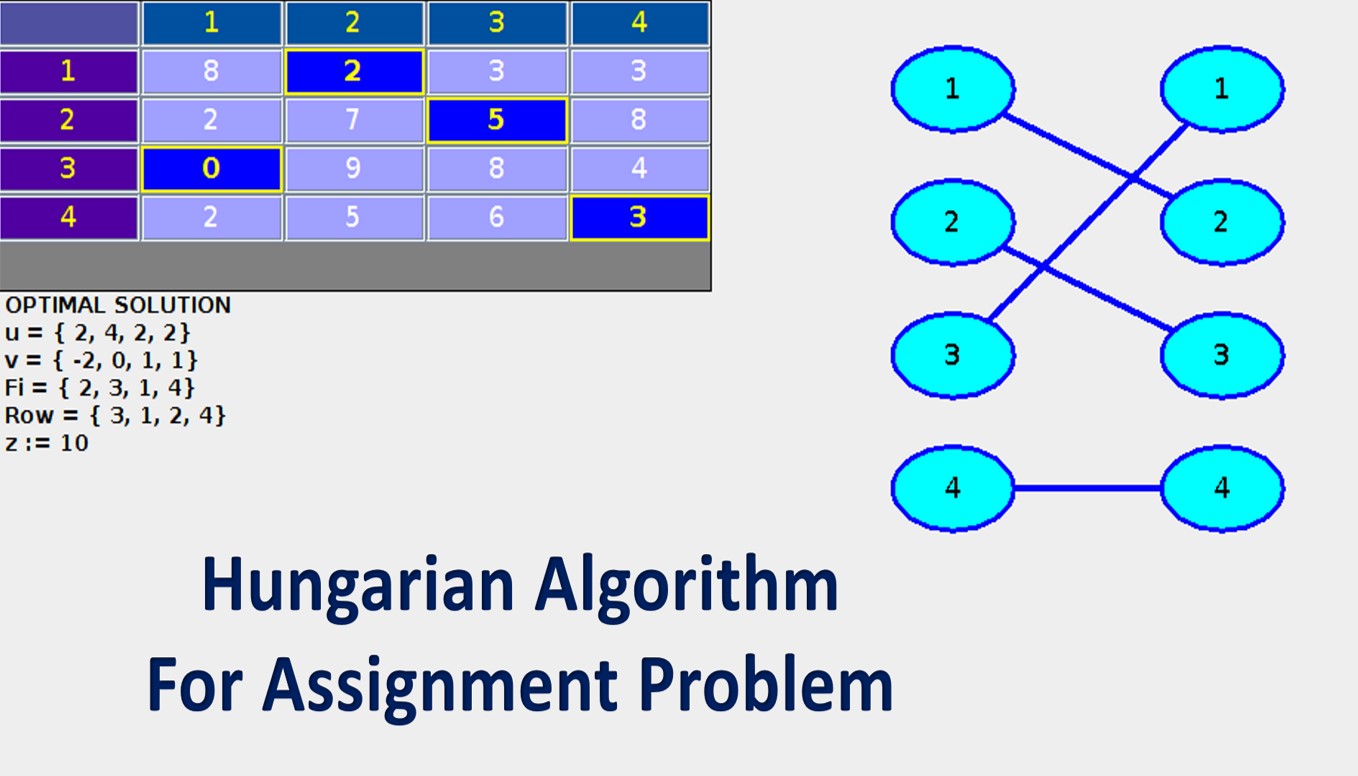
Hungarian Method Steps

The Hungarian calculation comprises of the four stages beneath. The initial two stages are executed once, while Steps 3 and 4 are rehashed until an ideal task is found. The contribution of the calculation is an n by n square framework with just non-negative components.

Stage 1: Subtract column minima

For each column, track down the most reduced component and take away it from every component in that line.

Stage 2: Subtract segment minima

Essentially, for every segment, track down the least component and take away it from every component in that section.

Stage 3: Cover every one of the zeros with a base number of lines

Cover every one of the zeros in the subsequent lattice utilizing a base number of level and vertical lines. In the event that n lines are required, an ideal task exists among the zeros. The calculation stops. On the off chance that not as much as n lines are required, go on with Step 4.

Stage 4: Create extra zeros

Track down the littlest component (call it k) that isn't canvassed by a line in Step 3. Take away k from every revealed component, and add k to all components that are covered two times.

Conclusion

The Hungarian matching calculation, additionally called the Kuhn-Munkres calculation that can be utilized to find most extreme weight matching’s in bipartite charts, which is some of the time called the task issue. A bipartite diagram can undoubtedly be addressed by a nearness network, where the loads of edges are the passages. Contemplating the chart as far as a contiguousness framework is helpful for the Hungarian calculation.

This strategy was created by, a Hungarian mathematician. To utilize this strategy, one has to be aware just the expense of making every one of the potential tasks. Every task issue has a lattice (table) related with it.